Tabla de Contenidos
Representación de números reales
Ya vimos en clases anteriores cómo se pueden representar números enteros y operar con ellos usando una cantidad fija de bits. En muchas aplicaciones es necesario representar números con decimales, números muy grandes que caen fuera del rango de representación de números enteros del procesador, o números muy cercanos a cero.
Representación de Punto Fijo
De la misma manera que podemos representar cierto rango de números enteros usando una cantidad fija de dígitos, es posible fijar además una cantidad de esos dígitos para representar la parte fraccionaria.
De esta manera podríamos representar un subconjunto de los números reales usando, por ejemplo, 8 dígitos, de los cuales 2 dígitos representan la parte fraccionaria. Luego los dígitos almacenados
12345678
representarían el valor 123456,78.
Es común usar estos tipos de datos para almacenar valores monetarios, evitando problemas de conversión de base y fijando la precisión. Por ejemplo el standard SQL define el tipo de datos DECIMAL(precision, escala), donde precision indica la cantidad de dígitos decimales (en base 10) y escala indica cuántos de ellos corresponden a la parte fraccionaria.
Sin embargo esta notación no es eficiente al momento de operar con números de magnitudes muy distintas, ya que requiere extender la precisión del resultado para no introducir errores por pérdida de dígitos significativos.
Notación científica
Una forma de representar números muy grandes, o muy pequeños de manera compacta es la notación científica. En vez de enumerar todos los dígitos que forman el número, éste se expresa como un valor multiplicado por una potencia de 10. Algunos ejemplos:
| 1,4959787 × 1011 m | Es la distancia promedio de la tierra al sol |
| 2,75 × 10-8 m | Diámetro de una molécula de agua |
| 6,02 × 1023 | Cantidad de moléculas en un mol de una substancia (número de Avogadro) |
De esta manera se pueden expresar números muy grandes o muy pequeños con una cantidad limitada de dígitos significativos, ya que la magnitud del número está dada por el exponente.
En general un número expresado en notación científica es de la forma +/- m × 10e donde m, llamado mantisa o significante, es un número real mayor o igual a uno y menor a 10, y el exponente e es un número entero.
Representación de Punto Flotante
La representación de números de punto flotante usa un esquema similar a la notación científica para representar números reales, definiendo una cantidad de dígitos para la mantisa y para el exponente.
Históricamente las computadoras implementaron este tipo de datos de distintas maneras, dificultando la transmisión de datos y la portabilidad de los algoritmos. Para corregir esta situación, el IEEE (Institute of Electrical and Electronics Engineers) elaboró un standard para normalizar la representación y la operación con datos de punto flotante. Al respetar el standard IEEE-754 los fabricantes de hardware y software pueden garantizar que representan los datos de la misma manera, con operaciones que funcionan correctamente.
Standard IEEE-754
Inicialmente el standard IEEE-754 definía tres formatos de punto flotante binario, que difieren básicamente en la cantidad de bits que utilizan para el exponente y la mantisa.
| Signo | Exponente | Mantisa | Total bits | |
| Precisión Simple | 1 bit | 8 bits | 23 bits | 32 |
| Precisión Doble | 1 bit | 11 bits | 52 bits | 64 |
| Precisión Extendida | 1 bit | 15 bits | 63 bits | 80 |
Los formatos de precisión simple y precisión doble corresponden a los tipos de datos float y double de los lenguajes C, C++ y java. El formato de precisión extendida es usado internamente por las unidades de punto flotante (FPU) para reducir el error introducido por la representación.
En este curso nos enfocaremos simplemente en la codificación y decodificación de números de punto flotante de Precisión Simple (32 bits).
Números normalizados
Dado que se trata de representaciones binarias, partiremos de la expresión binaria normalizada de un número real, es decir el número debe estar expresado de la siguiente manera:
x = (s) 1,m × 2e
Donde s representa el signo, m representa los dígitos de la parte fraccionaria, y el producto por 2e es la operación necesaria para que el valor normalizado sea igual al número original. Notar que el número debe tener un solo dígito distinto de cero en la parte entera. Esto implica que el cero no es un número normalizado, sino que tiene una representación especial.
Por ejemplo el número no normalizado 10101 es igual al valor normalizado 1,0101 × 24.
Consideraremos mantisa solamente a los dígitos binarios de la parte fraccionaria del número normalizado, asumiendo que la parte entera siempre vale 1.
- El signo del número completo se codifica con un bit de la siguiente manera
- s = 0: positivo
- s = 1: negativo
- El exponente se almacena como un número entero en exceso-n. La representación exceso-n permite almacenar números enteros como valores positivos, sumando una constante al valor original. En el caso de precisión simple, el exponente se almacena en exceso-127 (es decir, se le suma 127 y se almacena como un número binario positivo).
- En la mantisa se almacenan solamente los dígitos de la parte fraccionaria del número normalizado
Normalmente al operar con este tipo de datos estamos trabajando con números normalizados.
Valores especiales
Dado que la representación de punto flotante usa una cantidad acotada de bits, es imposible que pueda representar todos los números reales. En caso de que un número tenga demasiados dígitos significativos para ser representado exactamente, se utilizará la representación de punto flotante más cercana (Hay distintas formas de redondeo).
Las operaciones que produzcan valores demasiado grandes (overflow) se representan con el valor infinito. En caso de que el resultado sea demasiado pequeño (underflow), el resultado será un número desnormalizado, o directamente cero.
Además hay operaciones cuyo resultado no está definido o no es un número real, por ejemplo: 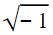 , 1/0, ln(-1). Estos casos estarán representados por el valor NaN (Not a Number).
, 1/0, ln(-1). Estos casos estarán representados por el valor NaN (Not a Number).
| Valor PF | Exponente | Mantisa |
| +/- cero | Exponente formado solo por ceros | Mantisa solo contiene ceros |
| Números desnormalizados | Exponente formado solo por ceros | Mantisa distinta de cero |
| +/- infinito | Exponente formado solo por unos | Mantisa solo contiene ceros |
| NaN | Exponente formado solo por unos | Mantisa distinta de cero |
De aquí surge que los exponentes formados solo por ceros y solo por unos no pueden utilizarse para representar números normalizados. En precisión simple, el menor exponente posible será -126 y el mayor 127.
Otra particularidad es que hay dos maneras de representar el cero, dependiendo del bit de signo: +0 y -0.
Codificación de un número en Punto Flotante de precisión Simple
De acuerdo con lo anterior, un número de punto flotante de precisión simple se codifica en 32 bits siguiendo el siguiente esquema:
| signo (1 bit) | exponente (8 bits) | mantisa normalizada (23 bits) |
Veamos cómo codificar un número cualquiera en Punto Flotante de precisión simple, por ejemplo: 534,5.
- En primer lugar debemos expresarlo como un número binario normalizado. Aplicando divisiones sucesivas y multiplicaciones sucesivas por 2 obtenemos que
534,510 = 1000010110,12
- Como la parte entera es mayor a 1, debemos normalizarlo. En este caso alcanza con dividirlo 9 veces por 2 para que solo quede un uno en la parte entera. Luego 534,510 = 1000010110,12 = 1,00001011012 × 29. Notar que si efectuamos el producto obtendremos el número original.
- Como el número es positivo, el bit de signo será s = 0.
- Codificamos el exponente 9 en exceso-127: 9 + 127 = 136 = 100010002
- Finalmente en los 23 bits de la mantisa se almacenan los dígitos de la parte fraccionaria, completando con ceros a la derecha en caso de que sean menos de 23. La representación binaria en punto flotante de 32 bits quedará así:

Dado que la representación de PF de 32 bits ocupa 4 bytes, es frecuente expresar el contenido de estos 4 bytes de manera más compacta en hexadecimal, de la misma manera que se visualiza el contenido de la memoria en hexadecimal.
En este caso los bits
0100 0100 0000 0101 1010 0000 0000 0000
se pueden expresar en hexadecimal de la siguiente manera:
44 05 A0 00
Decodificar un número de Punto Flotante de precisión simple
Suponiendo que obtenemos de la memoria 4 bytes que contienen un número real representado en punto flotante de precisión simple, podemos extraer el número que contiene siguiendo los pasos inversos.
Si el contenido de estos cuatro bytes expresado en hexadecimal es
BE 40 00 00
Debemos pasarlo a binario para poder extraer el signo, el exponente y la mantisa:
1011 1110 0100 0000 0000 0000 0000 0000
- Separando las partes quedará

- Como s=1, vemos que el número es negativo.
. - Como el exponente está codificado en exceso 127, podemos restarle 127 para obtener el exponente real:
- 011111002 = 64 + 32 + 16 + 8 + 4 = 124
- e = 124 - 127 = -3
.
- Podemos expresar el número binario normalizado reemplazando cada una de las partes
- f = (s) 1,m × 2e = -1,100000000000000000000002 × 2-3
- Desnormalizándolo queda: f = -0,00112
.
- Finalmente el valor del número de punto flotante expresado en decimal será
f = -0,00112 = -(1/8 + 1/16) = -(0,125 + 0,0625) = -0,187510
Consideraciones sobre la operación con números de punto flotante
Al tratarse de una representación finita de un conjunto infinito, hay que tener en cuenta que tanto la representación de números como las operaciones de punto flotante involucran un error en la mayoría de los casos. Esto puede provocar situaciones como la siguiente, por ejemplo en Python:
>>> 0.1 + 0.1 + 0.1 == 0.3 False
W8GBE6sdVuQ
Notar que la representación binaria de 0,1 requiere infinitos dígitos, por lo que el valor representado como 0.1 no es exactamente 0,1. Podemos ver la diferencia si mostramos el valor 0.1 con una cantidad grande de dígitos en la parte fraccionaria:
>>> '{0:.20g}'.format(0.1)
'0.10000000000000000555'
Esto sugiere que en muchos casos será un error comparar números de punto flotante usando la igualdad.
Además del error involucrado en la representación, cada operación de punto flotante introduce un error que es inevitable. Hay situaciones donde el orden en que se realicen las operaciones puede amplificar o disminuir el error. Por ejemplo restar dos números muy parecidos puede cancelar dígitos significativos magnificando el error.
eBkJilWMYvU Normalización en decimal
ijBLqXhq9RY Punto Flotante
